商空間檢視原始碼討論檢視歷史

商空間

來自 網絡 的圖片

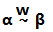商空間，設V是F-線性空間，W是V的一個子空間，對於任意的α，β向量屬於V，稱α與β關於W等價，當α - β屬於W。

簡介

(1)反身性 a~a

(2)對稱性 若a~b 則 b~a

(3)傳遞性 若a~b b~c則a~c。

評價

商空間的運算 和:(α + W)+(β + W)=(α + β)+ W

證明 a1 = α + W ; a2 = β + W,即 a1 - α 屬於W ，a2 - β 屬於W。 由於W為線性空間 故 (a1 - α)+(a2 - β)也屬於 W ，

(a1 - α)+(a2 - β)=(a1 + a2)- ( α + β )屬於W

即 a1 + a2 = (α + β) +W

數乘:k(α + W)=kα+W .證明類似和。

商空間的性質 商空間及上述定義的運算構成了一個線性空間。

V是一個n維線性空間 W是V的一個r維子空間 則V/W 為 n-r 維空間。