常模
| 常模 |
 |
|
中文名:常模 外文名:無 屬 性:標準量數 要 求:測驗分數必須與某種標準比較 |
常模是一種供比較的標準量數,由標準化樣本測試結果計算而來,即某一標準化樣本的平均數和標準差。它是人才測評用於比較和解釋測驗結果時的參照分數標準。測驗分數必須與某種標準比較,才能顯示出它所代表的意義。[1]
目錄
簡述
概念
測驗常模簡稱常模,即指一定人群在測驗所測特性上的普遍水平或水平分布狀況。可分為組間常模和組內常模兩大類。前者有年級、年齡常模,反映不同群體在測驗上表現的差異。後者有百分等級、標準分數、離差智商等常模。
常模的構成要素為:1、原始分數;2、導出分數;3、對常模團體的有關具體描述。[2]
建立步驟
①科學抽樣,從清楚而明確地定義的「特定人群」總體中,抽取到容量足夠大、並確具代表性的被試樣組
②要用擬建立常模的測驗,採用規範化施測手續與方法對標準化樣組(常模組)中的所有被試,施測該測驗,以便恰當而準確地收集到所有這些被試在該測驗上的實際測值
③對收集到的全部資料進行統計分析處理,真正把握被試樣組在該測驗上的普遍水平或水平分布狀況。
作用
常模的作用是讓測驗者明白測驗結果分數的意義。心理測驗是一種測量人的心理狀態的技術手段,如同一個醫生量一下你的血壓就可以知道你的血壓是否偏高偏低一樣,心理測驗也希望達到類似的心理測量的目的。
測驗者在人才測評系統中完成心理測驗以後,將會得到一個自己的位置,比如當你完成判斷推理測驗以後,可能被告知你的判斷推理能力要比75%的人都要高,你會不會覺得這是不可思議的呢?你會問,經過測驗就可以知道我會比多少人要高嗎?還是同樣的比喻,你為什麼會信任一個血壓計的指數?因為血壓計是客觀的,其實測驗的結果也是客觀的,兩者的結果都是以數值的形式表現,你之所以能夠從血壓計顯示的數值中了解自己的血壓是高了還是低了,那是因為你知道正常的血壓範圍是多少,這是一個比較的結果,將你自己的血壓與正常的血壓範圍進行比較,然後你得出了一個關於自己血壓的結論。
常模團體
性質
1、常模團體:是由具有某種共同特徵的人所組成的一個群體,或者是該群體的一個樣本。
2、常模團體在某方面的心理特質:常模是用一個標準的、規範的分數表示出來,以提供對個體作比較或評價的基礎。
3、任何一個測驗都有多個可能的常模團體。如智力測驗分兒童智力測驗和成人智力測驗。
4、對測驗編制者來說,常模的選擇主要基於對所要施測的總體的認識。團體常模團體必須能夠代表所要研究或施測的總體,具體工作包括:確定一般總體、確定目標總體、確定樣本
5、對測驗的使用者來說,要考慮的問題是,現有的哪個常模團體最適合。標準化測驗通常提供許多原始分數與各種常模的比較轉換表。有時能夠適用的常模團體不止一個。
6、常模團體的成員。
條件
1、群體的構成必須明確界定;定義常模團體的標準(變量)有:性別、年齡、職業、教育水平、社會經濟地位、種族等。
2、常模團體必須是所測群體的代表性樣本;
3、樣本大小要恰當:取樣誤差與樣本的大小成反比;樣本大小一般30—100,全國性2000—3000,最好為題量的5倍;樣本大小適當的關鍵是樣本要有代表性。
4、標準化樣組是一定時空的產物。
取樣方法
1、取樣:是指從總體(目標人群)中選擇有代表性的樣本。
2、分類:1)隨機取樣 2)非隨機取樣
3、具體取樣方法:
1)簡單隨機取樣:
概念:總體中每個個體均有獨立的等概率被被抽取的可能。
常用方法:抽籤法和隨機數字法(如從50 隨機選取10人)。
2)系統取樣:
概念:假設總體數目為N,選擇1/K的被試作為樣本,則樣本的大小(n)為:n = N×1/K(K = N/ n)給被試編號,按組距K分段,每段取1人。
注意事項:要求目標總體無序可循,也無等級結構存在,例如:從40人中抽取5人,從第3號開始抽取,為3、11、19、27、35
3)分組取樣:如:按個方麵條件基本相同的學校取樣
適用於:總體數目大,而且群體有多樣性,將群體分組,在組內隨機取樣。
注意事項:要求儘可能減小組間差異,儘量加大組內差異
4)分層取樣:
方法:將目標群體按某種變量(如年齡)分成若干層次,再從各層次中隨機抽取若干被試。
特點:使各層次差異顯著。同層次保持一致,增加了樣本的代表性注意事項:要求儘可能加大層次間的差異,儘量減小層次內的差異。
分類: (1)分層比例取樣:(2)分層非比例取樣:各層次的差異很大時採用。
常模分數與常模
1、常模分數:就是施測常模樣本後,將被試者的原始分數按一定規則轉換出來的導出分數。 原始分數:是指被試者的反應與標準答案相比較而獲得的測驗分數。
導出分數:原始分數本身沒有多大意義,必須有一個參照標準才行,在心理測驗中,這種標準是由原始分數構成的分布轉換而來的分數,叫導出分數。導出分數具有一定的對照點和單位,它實際上是一個有意義的測驗量表,它與原始分數等值,可以進行比較。
2、常模:就是常模分數構成的分布,它是解釋心理測驗分數的基礎。
一般常模:常為測驗指導書上列出的常模。
特殊常模:為非典型群體建立的,如某個單位。特殊常模的建立方法:根據樣本的原始分數製作次數分布圖,再計算出導出分數,最後製成轉換表。
常模類型
發展常模
就是根據不同年齡上各種發展水平的人的平均表現(如智力、技能、感覺運動等方面的發展水平)所制定的量表。
1、發展順序量表:與發育正常的兒童相比,按年齡評定一個兒童的心理發展水平。
1)葛爾塞發展程序量表:按月份顯示發育正常兒童在運動水平、適應性、語言、社會性四個方面的發展水平,以此作為標準,評定個體的發展水平。強調兒童早期行為的發展是有規律的。
2)皮亞傑的發展理論——對守恆概念的研究:5歲時才會理解質量守恆;6歲才會掌握重量守恆;7歲時才有容量守恆概念。(守恆:是指二種等量的物體,只要無增無減,無論怎麼組合,它們在質量、重量、長度、數量及容量等方面仍然是相等的。)
2、智力年齡(個體的智力所達到的年齡水平——智齡)。智力年齡是指一個兒童在年齡量表上所得的分數。
1)比內-西蒙智力量表——首先使用智力年齡的概念;智齡是年齡量表上度量智力的單位。編制出可區分各年齡兒童的智力水平的測題,這些測題的難度隨年齡而逐漸加大。
2)為每個年齡水平都編制一些適當的題目,其中的每個測題是該年齡組大部分兒童都能完成的。以智力年齡(智齡)作為度量智力的單位。
3)智力年齡的計算方法:
範例:吳天敏修訂的比內-西蒙智力量表:每個年齡組各有6個測題,每答對一題增加智齡2個月。先確定基礎年齡(智力量表中全部被通過的那一組測題所代表的年齡)。
例如:六歲組的測題全部答對,更高年齡組的測題只有部分答對,或都未通過,則基礎年齡為六歲,再求答對的更高年齡組上的測題數量,每答對一題增加智齡2個月。
智力年齡=基礎年齡+更高年齡組上通過的測題數量所代表的智齡增長的月數
3、測定智力年齡的另一種方法——測題不分年齡組
以標準化樣本中每個年齡組的平均分數作為年齡常模
將個人的原始分數與年齡常摸作比較,計算其智力年齡
4、年級當量——實際上就是年級量表。將一個學生和同年級學生相比。年級量表的單位通常為10個月間隔(故10個月為一個學年)。
百分位常模
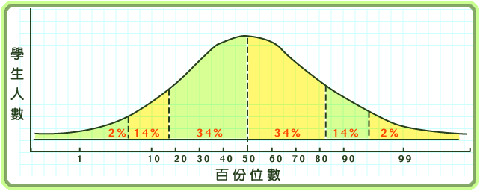
1、百分等級:
1)是應用最廣的表示測驗分數的方法;
2)一個測驗分數的百分等級是指在常模樣本中低於該分數的人數百分比;即百分等級指出的是個體在常模團體中所處的位置,百分等級越低,個體所處的位置就越低;
3)分類:
(1)未分組資料的百分位數:計算:PR = 100 -(100R-50)/N R是原始分數排列順序,N是指總人數(樣本的總人數)
(2)分組資料的百分等級:
2、百分點(百分位數):是計算處於某一百分比例的人對應的測驗分數是多少;是分數量表上相對於某一百分等級的分數點,又稱百分位數(PP)根據直線內插法計算(舉例:高考成績):(100-百分等級)/(最高分-PP)=(百分等級-1/PP-最低分)
原始分數和百分等級可互相轉換,由此編制的原始分數與百分等級的對照表,稱為百分位常模。
3、四分位數和十分位數
1)四分位數:將分數量表分成四等份,相當於百分等級的25%、50%和75%三個百分點分成的四段;
2)十分位數:將分數量表分為十段:10%、20%等。
標準分數
1、是將原始分數與平均數的距離以標準差為單位表示出來的量表;
2、其基本單位是標準差;
3、常用的標準分數有:z分數、Z分數、T分數、標準九分數、離差智商(IQ)等。
4、分類:
1)線性轉換的標準分數:
(1)適用於正態(常態)分布的數據資料;
(2)z分數為最典型的線性轉換的標準分數;
(3)z分數:z =(X-M)/SD
X為任一原始分數,M為樣本平均數,SD為樣本標準差。
z分數可以用來表示某一分數與平均數之差是標準差的幾倍。
(4)轉換後的Z分數:Z=A+Bz
Z為轉換後的標準分數,A、B為根據需要指定的常數;加上一個常數是為了去掉負值,乘以一個常數是為了使單位變小而去掉小數點;加或乘一個常數並不改變原來分數間的關係。
2)非線性轉換的標準分數:
(1)原始分數不是常態分布——使之常態化(常態化過程是非線性的);
(2)常態化過程主要是將原始分數轉化為百分等級,再將百分等級轉化為常態分布上相應的離均差,並可以表示為任何平均數和標準差。
(3)計算步驟:
A、對每個分數值計算累積百分數
B、在常態曲線面積中,求出對應的該百分比的z分數 所得的z分數可將分布分成幾部分,稱之為z'分數,以區別線性轉換所求得的z分數。 與線性導出分數一樣,常態化標準分數也可以被轉化為任何方便的形式,並可用以下表示:
C、T分數——以50為平均數(即加上一個常數50),以10為標準差(乘以一個常數理10),即: T= 50 +10 z' (平均數為50,標準差為10)
D、標準九分:其量表是個9級分數量表(平均數為5,標準差為2)
E、標準十分——平均數為5.5,標準差為1.5; 標準二十分——平均數為10,標準差為3。 (使用最廣、影響最大的一種常態化標準分數是離差智商)
建立標準分數常模步驟。
我們要為性能優良的測驗建立標準分數常模步驟①從明確界定好的該測驗應該測查的被試總體中,抽取一個容量足夠大的代表性樣組,即建立起常模組(常模團體)②對該代表性樣組按應有規範施測該測驗,獲得代表性樣組中每一被試的測驗分數,即得到常模團體的測驗分數組③求取常模團體測驗分數組的平均數與標準差,按公式求取從-3.000到3.000這一區間上若干個點的標準分數(Z值)跟測驗原始分數的對照表,就得到了標準分數常模表。
離差智商及含義
在最早的比內—西蒙智力測驗中沒有智商的概念,只用「心理年齡」(MA)來表示被試智力的高低。當前一般都用比率智商和離差智商來表示智力的高低。
1、比率智商(IQ):為心理年齡(MA)與實足年齡(CA)之比。為避免小數,將商數乘以100。計算公式IQ = MA/CA×100
如果一個兒童的心理年齡等於實足年齡,他的智商就100。IQ等於100代表正常的或平常的智力。 比率智商並不適合於年齡較大的被試。
2、離差智商:是一種以年齡組為樣本計算而得的標準分數; 韋克斯勒將離差智商的平均數定為100,標準差為15;離差智商表示的是個體智力在年齡組中所處的位置;是表示智力高低的一種理想指標。
計算公式:IQ=100+15z'=100+15(X-M)/SD
X表示被試的量表分數,M表示被試所在年齡水平的平均量表分數,SD表示這一年齡水平被試的量表分數的標準差。將原始分與IQ值的對應關係計算出來作為常模表(P344表)。
韋克斯納:平均數定為100,標準差為15
斯-比測驗:平均數為100,標準差為16
表達方法
轉換表法
——是最簡單而且最基本的表示常模的方法。
1、一個轉換表顯示出一個特定的標準化樣組的原始分數與其對應的等值分數——百分位、標準分數、T分數或其他任何分數。利用轉換表可將原始分數轉換為與其對應的導出分數,從而對測驗的分數作出有意義的解釋。
2、簡單的轉換表就是將單項測驗的原始分數轉換成一種或幾種導出分數。複雜的轉換表通常包括幾個分測驗或幾種常模團體的原始分數與導出分數的對應關係。 剖面圖
——是將測驗分數的轉換關係用圖形表示出來。可以很直觀地看出被試在各分測驗上的表現及其相對位置。
標準差代表一組數據的離散程度,如一個班內學生數學成績的離散程度從理論上說,心理測量數據一般服從為正態分布,或接近正態分布。正態分布曲線的形狀取決於標準差,但曲線下的面積始終為1個單位在心理測量中,個體在團體中的相對位置,以Z分數的大小表示,而Z分數是標準差作為單位,既以包含幾個標準差表示個體分數與總體平均分數的距離,而不是用兩者的絕對分數之差表示表示個體在團體中的相對位置。 根據Z分數可確定低於或某或高於某個分數的人數比例,也可以對不同的測量結果進行比較心理統計基本知識。
參考資料
- ↑ 我國軍人症狀自評量表常模的建立及其結果分析,CNKI知網空間
- ↑ SCL-90信度效度檢驗和常模的再比較,萬方數據