線性方程組
| 線性方程組 |
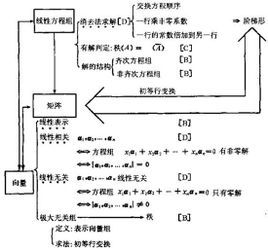 |
線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。
簡介
xj表未知量,aij稱係數,bi稱常數項。
稱為係數矩陣和增廣矩陣。若x1=c1,x2=c2,…,xn=cn代入所給方程各式均成立,則稱(c1,c2,…,cn)為一個解。若c1,c2,…,cn不全為0,則稱(c1,c2,…,cn)為非零解。若常數項均為0,則稱為齊次線性方程組,它總有零解(0,0,…,0)。兩個方程組,若它們的未知量個數相同且解集相等,則稱為同解方程組。線性方程組主要討論的問題是:①一個方程組何時有解。②有解方程組解的個數。③對有解方程組求解,並決定解的結構。這幾個問題均得到完滿解決:所給方程組有解,則秩(A)=秩(增廣矩陣);若秩(A)=秩=r,則r=n時,有唯一解;r<n時,有無窮多解;可用消元法求解。
當非齊次線性方程組有解時,解唯一的充要條件是對應的齊次線性方程組只有零解;解無窮多的充要條件是對應齊次線性方程組有非零解。但反之當非齊次線性方程組的導出組僅有零解和有非零解時,不一定原方程組有唯一解或無窮解,事實上,此時方程組不一定有 ,即不一定有解。
克萊姆法則(見行列式)給出了一類特殊線性方程組解的公式。n個未知量的任一齊次方程組的解集均構成n維空間的一個子空間。
線性方程組有廣泛應用,熟知的線性規劃問題即討論對解有一定約束條件的線性方程組問題。
評價
線性方程組的解法,早在中國古代的數學著作《九章算術》方程章中已經作了比較完整的論述。其中所述方法實質上相當於現代的對方程組的增廣矩陣的行施行初等變換,消去未知量的方法。在西方,線性方程組的研究是在17世紀後期由萊布尼茨開創的。他曾研究含兩個未知量的三個線性方程組成的方程組,證明了當方程組的結式等於零時方程有解。馬克勞林在18世紀上半葉研究了具有二、三、四個未知量的線性方程組,得到了現在稱為克萊姆法則的結果,克萊姆不久也發表了這個法則。18世紀60年代以後,法國數學家貝祖對線性方程組理論進行了一系列研究,證明了n元齊次線性方程組(n個方程)有非零解的條件是係數行列式等於零。他還利用消元法將高次方程問題與線性方程組聯繫起來,提供了某些n次方程的解法。
到了19世紀,英國數學家H.J.S.史密斯和道奇森繼續研究線性方程組理論,前者引進了方程組的增廣矩陣和非增廣矩陣的術語,後者證明了n個未知數m個方程的方程組相容的充要條件是非增廣矩陣和增廣矩陣中的最高階非零行列式是同階的,即兩個矩陣的秩相同,這正是現代解方程組的條件。
大量的科學技術問題,最終往往歸結為解線性方程組,因此線性方程組的數值解法得到發展,並在計算數學中占有重要地位。[1]