狄拉克方程檢視原始碼討論檢視歷史
| 狄拉克方程 |
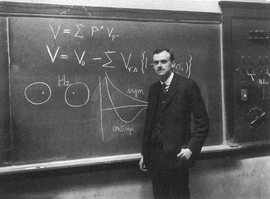 |
1928年英國物理學家狄拉克即狄拉克方程。利用這個方程研究氫原子能級分布時,考慮有自旋角動量的電子作高速運動時的相對論性效應,給出了氫原子能級的精細結構,與實驗符合得很好。從這個方程還可自動導出電子的自旋量子數應為1/2,以及電子自旋磁矩與自旋角動量之比的朗德g因子為軌道角動量情形時朗德g因子的2倍。電子的這些性質都是過去從分析實驗結果中總結出來的,並沒有理論的來源和解釋。狄拉克方程卻自動地導出這些重要基本性質,是理論上的重大進展。
簡介
狄拉克方程的形式如圖示一。理論物理中,相對於薛定諤方程之於非相對論量子力學,狄拉克方程是相對論量子力學的一項描述自旋-½粒子的波函數方程,由英國物理學家保羅·狄拉克於1928年建立,不帶矛盾地同時遵守了狹義相對論與量子力學兩者的原理,實則為薛定諤方程的洛倫茲協變式。這條方程預言了反粒子的存在,隨後1932年由卡爾·安德森發現了正電子(positron)而證實。負能量態的存在意味着物質是不穩定的,因為電子會不斷向負能量的狀態躍遷而不斷輻射能量出來,這是一個近乎荒謬的結論。為了解決這個困難,狄拉克提出真空狀態充滿了負能量的電子「海」,因為這些負能的狀態已經被電子占領,正能量的電子就無法向這些負能狀態躍遷。狄拉克還發現,如果「海」中的電子被「打」掉就等價於形成了一個帶正電荷的粒子。後來人們認識到這樣的「空穴」應該和電子具有相同的質量,這就是正電子的最初的來源。
評價
為了更好的理解這個說法,以牛頓定律為例舉一個例子。牛頓第二定律說物體的加速度和所受到的外力成正比,即F=ma。如果用微分方程表示,加速度可以表示為時間t的二次微分,也就是說,在這個方程里,代入「t」和「-t」得出的結果是一樣的。如果地球繞着太陽的運動滿足牛頓第二定律,那麼時間反演一下,相當於地球沿着和現在的軌道相反的路徑運行,也同樣滿足牛頓第二定律。現在地球的運動軌跡和與此完全相反的軌跡都是上面牛頓方程的解。同樣我們可以這樣理解,當把電子的電荷反演一下,它們都是狄拉克方程的解。[1]