勻速圓周運動檢視原始碼討論檢視歷史
| 勻速圓周運動 |
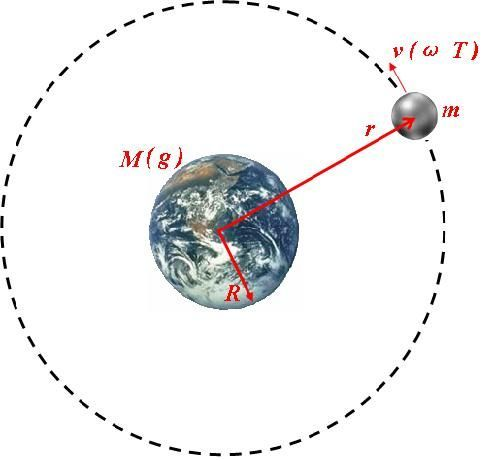 |
勻速圓周運動,質點沿圓周運動,如果在任意相等的時間裡通過的圓弧長度都相等,這種運動就叫做「勻速圓周運動」,亦稱「勻速率圓周運動」。因為物體作圓周運動時速率不變,但速度方向隨時發生變化。所以勻速圓周運動的線速度是無時無刻不在變化的。
簡介
質點沿圓周運動,如果在相等的時間裡通過的圓弧長度相等,這種運動就叫做勻速圓周運動。
勻速圓周運動是最簡單的圓周運動形式,也是最基本的曲線運動之一。勻速圓周運動是一種理想化的運動形式。許多物體的運動接近這種運動,具有一 定的實際意義。一般圓周運動,也可以取一段較短的時間(或弧長)看成是勻速圓周運動。
勻速圓周運動應理解為「勻速率」圓周運動。因為「在相等的時間裡通過的圓弧長度相等」,指的是速率不變。
勻速圓周運動從力的角度來看是只受一個指向圓心的力〔或合力〕
勻速圓周運動保持加速度大小不變,方向時刻改變
評價
任何物體在作圓周運動時需要一個向心力,因為它在不斷改變速度。對象的速度的速率大小不變,但方向一直在改變。只有合適大小的向心力才能維持物體在圓軌道上運動。這個加速度(速度是一個矢量,改變方向的同時可以不改變大小)是由向心力提供的,如果不具備這一條件,物體將脫離圓軌道。注意,向心加速度是反映線速度方向改變的快慢。
物體在作圓周運動時速度的方向相切於圓周路徑。勻速圓周運動物體所受合力的方向一直指向圓心,即此來改變速度的方向。
現在,向心力可以使物體不脫離軌道。一個很好的例子是重力。 地面重力給人造衛星必要的力使其在沿軌道運動。
現在回到物理學上來。向心力與物體速度的平方及它的質量和半徑倒數成正比: F = mv²/r,F=mω²r(v是線速度,ω是角速度)
所以如果我們知道了力大小,質量,半徑,我們可以算出對象旋轉速度。 如果我們知道了速度,質量,半徑,我們可以算出力大小。符號記為如下:
F = ma
是的,合外力=質量乘以加速度,所以: a = v²/r =(2π)²r/T²
質量符號去除—用 F和 ma 取代. 因此求加速度可以不用知道物體的質量。
當一質點在一平面做圓周運動時在另一正交平面的射影是做簡諧運動,與彈簧振子的運動形式一樣,加速度在不斷變化中。
如果物體沿半徑是R的圓周作勻速圓周運動,運動一周的時間為T,則線速度的大小等於角速度大小和半徑R的乘積. v=ωR,使用這一公式時應注意,角度的單位一定要用弧度,只有角速度的單位是弧度/秒時,上述公式才成立.[1]