全微分檢視原始碼討論檢視歷史

全微分

來自 網絡 的圖片

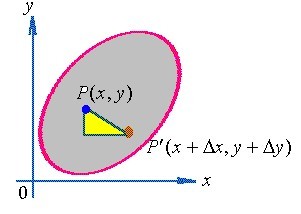全微分，如果函數z=f(x, y) 在(x, y)處的全增量△z=f(x+△x，y+△y)-f(x,y)可以表示為△z=A△x+B△y+o(ρ)，其中A、B不依賴於△x, △y，僅與x,y有關，ρ→0，此時稱函數z=f(x, y)在點（x，y）處可微分，A△x+B△y稱為函數z=f(x, y)在點(x, y)處的全微分，記為dz即dz=A△x +B△y。 該表達式稱為函數z=f(x, y) 在(x, y)處(關於△x, △y)的全微分。

簡介

函數z=f(x, y) 的兩個偏導數f'x(x, y), f'y(x, y)分別與自變量的增量△x, △y乘積之和

f'x(x, y)△x + f'y(x, y)△y

若該表達式與函數的全增量△z之差，

當ρ→0時，是ρ( )的高階無窮小，

那麼該表達式稱為函數z=f(x, y) 在(x, y)處(關於△x, △y)的全微分。

記作：dz=f'x(x, y)△x + f'y(x, y)△y

評價

定理1 如果函數z=f（x，y）在點p0（x0，y0）處可微，則z=f（x，y）在p0（x0，y0)處連續，且各個偏導數存在，並且有f′x（x0，y0）=A，f′y（x0，y0）=B。 定理2 若函數z=f（x，y）在點p0（x0，y0）處的偏導數f′x，f′y連續，則函數f在點p0處可微。