伴隨矩陣檢視原始碼討論檢視歷史
| 伴隨矩陣 |
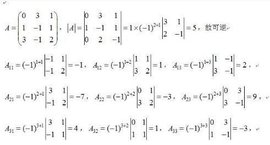 |
在線性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果矩陣可逆,那麼它的逆矩陣和它的伴隨矩陣之間只差一個係數。然而,伴隨矩陣對不可逆的矩陣也有定義,並且不需要用到除法。
簡介
① 當矩陣是大於等於二階時:主對角元素是將原矩陣該元素所在行列去掉再求行列式.非主對角元素 是原矩陣該元素的共軛位置的元素去掉所在行列求行列式乘以(-1)^(x+y) x,y為該元素的共軛位置的元素的行和列的序號,序號從1開始的.主對角元素實際上是非主對角元素的特殊情況,因為x=y,所以(-1)^(x+y)=(-1)^(2x)=1,一直是正數,沒必要考慮主對角元素的符號問題。常用的可以記一下:a b—— 1/(ad-bc) (d -c c d -b a)②當矩陣的階數等於一階時,他的伴隨矩陣為一階單位方陣.3.二階矩陣的求法口訣:主對角線對換,副對角線符號相反。
評價
伴隨矩陣的求法:主對角元素是將原矩陣該元素所在行列去掉再求行列式;非主對角元素,是原矩陣該元素的共軛位置的元素去掉所在行列求行列式乘以(-1)^(x+y),x,y為該元素的共軛位置的元素的行和列的序號,序號從1開始的。伴隨矩陣是一種特殊矩陣,它和矩陣的逆矩陣有着緊密的聯繫,方陣的伴隨矩陣是在求可逆矩陣的逆矩陣時提出來的,是大學數學學習的重點和難點,而且也有很多的應用價值,和數學其他分支的聯繫也很廣泛。伴隨矩陣是矩陣理論及線性代數中的一個基本概念,是許多數學分支研究的重要工具,伴隨矩陣的一些新的性質被不斷發現與研究。[1]