秩和检验查看源代码讨论查看历史
| 秩和检验 |
 |
秩和检验,在实践中我们常常会遇到以下一些资料,如需比较患者和正常人的血清铁蛋白、血铅值、不同药物的溶解时间、实验鼠发癌后的生存日数、护理效果评分等,我们将非参数统计中一种常用的检验方法--秩和检验,其中"秩"又称等级、即上述次序号的和称"秩和",秩和检验就是用秩和作为统计量进行假设检验的方法。
简介
问题的提出
在实践中我们常常会遇到以下一些资料,如需比较患者和正常人的血清铁蛋白、血铅值、不同药物的溶解时间、实验鼠发癌后的生存日数、护理效果评分等,这类资料有如下特点:
(1)资料的总体分布类型未知;
(2)资料的总体分布类型已知,但不符合正态分布;
(3)某些变量可能无法精确测量;
(4)方差不齐。
对于此类资料,除了进行变量变换或t'检验外,可采用非参数统计方法。
参数统计与非参数统计的区别
参数统计:即总体分布类型已知,用样本指标对总体参数进行推断或作假设检验的统计分析方法。
非参数统计:即不考虑总体分布类型是否已知,不比较总体参数,只比较总体分布的位置是否相同的统计方法。
评价
多个样本两两比较的秩和检验
同样的,多个样本组比较的秩和检验,如拒绝H0,只说明比较各组的总体分布位置不同或不全相同,应在此基础上进行两两比较,常用Nemenyi法。
秩和检验的优缺点
秩和检验的优点是(1)不受总体分布限制,适用面广;(2)适用于等级资料及两端无确定值的资料;(3)易于理解,易于计算。缺点是符合参数检验的资料,用秩和检验,则不能充分利用信息,检验功效低。
3.应用中的注意事项:
(1)注意应用条件;
(2)编秩时相同值要取平均秩次;
(3)相同秩次较多时,统计量要校正。
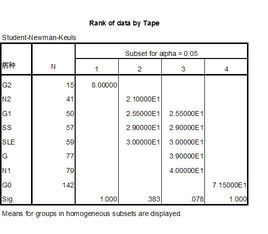
秩和检验常用软件
spss软件,只要输入数据,选择合适的参数,就可以很快得到结果。[1]