黑体辐射
本条目存在以下问题,请协助改善本条目或在讨论页针对议题发表看法。
|
 |
黑体辐射指处于热力学平衡态的黑体发出的电磁辐射。黑体辐射的电磁波谱只取决于黑体的温度。
另一方面,所谓黑体辐射其实就是光和物质达到平衡所表现出的现象。物质达到平衡,所以可以用一个温度来描述物质的状态,而光和物质的交互作用很强,如此光和光之间也可以用一个温度来描述(光和光之间本身不会有交互作用,但光和物质的交互作用很强)。而描述这关系的便是普朗克分布[1] (Planck distribution)。黑体辐射能量按波长的分布仅与温度有关。
黑体不仅仅能全部吸收外来的电磁辐射,且散射电磁辐射的能力比同温度下的任何其它物体强。
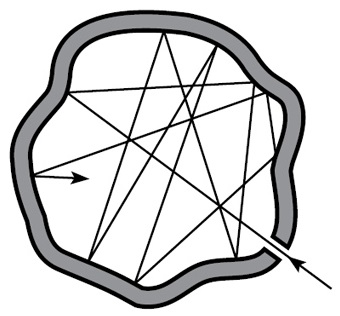
对于黑体的研究,使自然现象中的量子效应被发现。 黑体作为一个理想化的物体,在现实中是不存在的,因此现实中物体的辐射也与理论上的黑体辐射有所出入。但是,可以观察一些非常类似黑体的物质发出的辐射,例如一颗恒星或一个只有单一开口的空腔所发出的辐射。举个例来说,人们观测到宇宙背景辐射,对应到一个约3K的黑体辐射,这暗示宇宙早期光是和物质达到平衡的。而随著时间演化,温度慢慢降了下来,但方程式依然存在。(频率和温度的效应抵销)
目录
行星和其卫星之间的热力学关系
黑体辐射定理的应用之一是用于概略的估计一个行星的温度。其表面可能由于温室效应而比估计温度高。
因素
行星的温度主要和以下几个因素相关:
所有的辐射,无论是行星内部产生的,其他恒星还是其本身放出的,对行星的温度都有很重要的影响。以下的推导即著重讨论辐射。
推导
首先使用斯特藩-玻尔兹曼定律得到太阳放射出的总功率(能量/秒):
- P_{S emt} = \left( \sigma T_{S}^4 \right) \left( 4 \pi R_{S}^2 \right) \qquad
- \sigma \,:斯特藩-玻尔兹曼常数
- T_S \,: 太阳的表面温度
- R_S \,: 太阳的半径
太阳平均的向各个方向放出能量,因此,地球实际上只是接受到其中很小的一部分。这部分能量为(指接触到大气层外部):
- P_{SE} = P_{S emt} \left( \frac{\pi R_{E}^2}{4 \pi D^2} \right) \qquad
其中
- R_{E} \, :地球的半径
- D \,:天文单位, 太阳与地球的平均距离
由于本身的高温,太阳发出的射线大多数属于紫外线和可见光(UV-Vis)频率范围。在这个频率范围内,地球会反射一部分能量,其数量为alpha,即地球对UV-Vis范围射线的反照率。反过来,即地球吸收了1-\alpha的太阳光,并反射了剩下的。地球和其大气层所吸收的能量为:
- P_{abs} = (1-\alpha)\,P_{SE} \qquad \qquad
虽然地球仅仅以一个面积为\pi R^2的圆形区域进行吸收,但是它同时以一个球体的形态向各个方向放出能量。假设地球是一个完全黑体,它将遵循斯特藩-玻尔兹定理:
- P_{emt\,bb} = \left( \sigma T_{E}^4 \right) \left( 4 \pi R_{E}^2 \right) \qquad \qquad
其中T_{E} 是地球的温度。由于地球的温度明显低于太阳,其放射的多为光系的红外线(IR)部分。在这个频率范围内,地球会放出黑体总放射波的一部分,大约为\overline{\epsilon},\overline{\epsilon}是红外线频率的平均放射率。因此地球和其大气层实际放出的能量为:
- P_{emt} = \overline{\epsilon}\,P_{emt\,bb} \qquad
假设地球处于热平衡,则吸收的能量等于放射的能量:
- P_{abs}=P_{emt} \qquad \qquad
代入所有关于太阳和地球能量的表达式(1-5)可以得到:
- T_E=T_S\sqrt{\frac{R_S\sqrt{\frac{1-\alpha}{\overline{\epsilon}}}}{2D}
换句话说,考虑到所有的估计值,地球的温度与下列因素有关:太阳的表面温度,太阳的半径,日地间距,以及地球的反照率和红外发射率。
地球的温度
如果代入对太阳和地球的测量值:
- T_{S} = 5778 \ \mathrm{K},
- R_{S} = 6.96 \times 10^8 \ \mathrm{m},
- D = 1.496 \times 10^{11} \ \mathrm{m},
- alpha = 0.306 \
并将平均放射率设为单位量,可以得到地球的“有效温度”为:
- T_E = 254.356 K or -18.8 ℃.
这个温度值是基于地球是一个完全黑体的假设,忽略温室效应并认为地球的反照率完全不变的基础上得到的。而实际上地球仅是非常接近一个完美黑体,所以必须将估计温度定为比有效温度高出好几度。如果想要估计地球在没有大气层的情况下的温度,可以使用月球的反照率和发射率进行计算。月球的反照率和发射率大约为0.1054和0.95, 因此,可以得到这种情况下的温度约为1.36 ℃. 地球的平均反照率的估计值在0.3–0.4之间,由此可以得到不同的估计温度。进行计算时相较于太阳的温度,尺寸和日地距离,人们更加常用日照常量(总日照量密度)。比如使用0.4为反照率并使用日照量密度1400 W m−2,可以得到约为245K的地球温度。
运动黑体的多普勒效应
多普勒效应是著名的物理现象,人们用它来描述当一个光源对观察者作相对运动时,其光线频率的变化。若一单色光源的发射频率为f,则当它相对观察者做相对运动时,观察者看起来其频率为f':
- f' = f \frac{1}{\sqrt{1-v^2/c^2}} (1 - \frac{v}{c} \cos \theta)
其中v是这个光源对观察者的相对速度,θ是速度向量和观察者及光源间连线的夹角,c为光速。上面的公式为总公式,还可以从其得到一些更简单的特殊例子,如光源直接向观察者移动(θ = π) 或是离开观察者(θ = 0),当然其移动速度远远小于c。