聚類
| 聚類 |
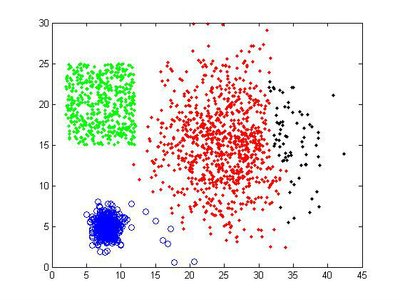 |
聚類 將物理或抽象對象的集合分成由類似的對象組成的多個類的過程被稱為聚類。由聚類所生成的簇是一組數據對象的集合,這些對象與同一個簇中的對象彼此相似,與其他簇中的對象相異。"物以類聚,人以群分",在自然科學和社會科學中,存在着大量的分類問題。聚類分析又稱群分析,它是研究(樣品或指標)分類問題的一種統計分析方法。聚類分析起源於分類學,但是聚類不等於分類。聚類與分類的不同在於,聚類所要求劃分的類是未知的。聚類分析內容非常豐富,有系統聚類法、有序樣品聚類法、動態聚類法、模糊聚類法、圖論聚類法、聚類預報法等。 [1]
在數據挖掘中,聚類也是很重要的一個概念。
目錄
基本信息
典型應用
"聚類的典型應用是什麼?"在商務上,聚類能幫助市場分析人員從客戶基本庫中發現不同的客戶群,並且用購買模式來刻畫不同的客戶群的特徵。在生物學上,聚類能用於推導植物和動物的分類,對基因進行分類,獲得對種群中固有結構的認識。聚類在地球觀測數據庫中相似地區的確定,汽車保險單持有者的分組,及根據房子的類型、價值和地理位置對一個城市中房屋的分組上也可以發揮作用。聚類也能用於對Web上的文檔進行分類,以發現信息。
典型要求
可伸縮性:許多聚類算法在小於 200 個數據對象的小數據集合上工作得很好;但是,一個大規模數據庫可能包含幾百萬個對象,在這樣的大數據集合樣本上進行聚類可能會導致有偏的結果。我們需要具有高度可伸縮性的聚類算法。
處理不同類型數據的能力:許多算法被設計用來聚類數值類型的數據。但是,應用可能要求聚類其他類型的數據,如二元類型(binary),分類/標稱類型(categorical/nominal),序數型(ordinal)數據,或者這些數據類型的混合。
發現任意形狀的聚類:許多聚類算法基於歐幾里得或者曼哈頓距離度量來決定聚類。基於這樣的距離度量的算法趨向於發現具有相近尺度和密度的球狀簇。但是,一個簇可能是任意形狀的。提出能發現任意形狀簇的算法是很重要的。
用於決定輸入參數的領域知識最小化:許多聚類算法在聚類分析中要求用戶輸入一定的參數,例如希望產生的簇的數目。聚類結果對於輸入參數十分敏感。參數通常很難確定,特別是對於包含高維對象的數據集來說。這樣不僅加重了用戶的負擔,也使得聚類的質量難以控制。
處理"噪聲"數據的能力:絕大多數現實中的數據庫都包含了孤立點,缺失,或者錯誤的數據。一些聚類算法對於這樣的數據敏感,可能導致低質量的聚類結果。
對於輸入記錄的順序不敏感:一些聚類算法對於輸入數據的順序是敏感的。例如,同一個數據集合,當以不同的順序交給同一個算法時,可能生成差別很大的聚類結果。開發對數據輸入順序不敏感的算法具有重要的意義。
高維度(high dimensionality):一個數據庫或者數據倉庫可能包含若干維或者屬性。許多聚類算法擅長處理低維的數據,可能只涉及兩到三維。人類的眼睛在最多三維的情況下能夠很好地判斷聚類的質量。在高維空間中聚類數據對象是非常有挑戰性的,特別是考慮到這樣的數據可能分布非常稀疏,而且高度偏斜。
基於約束的聚類:現實世界的應用可能需要在各種約束條件下進行聚類。假設你的工作是在一個城市中為給定數目的自動提款機選擇安放位置,為了作出決定,你可以對住宅區進行聚類,同時考慮如城市的河流和公路網,每個地區的客戶要求等情況。要找到既滿足特定的約束,又具有良好聚類特性的數據分組是一項具有挑戰性的任務。
可解釋性和可用性:用戶希望聚類結果是可解釋的,可理解的,和可用的。也就是說,聚類可能需要和特定的語義解釋和應用相聯繫。應用目標如何影響聚類方法的選擇也是一個重要的研究課題。
計算方法
傳統的聚類分析計算方法主要有如下幾種:
1、劃分方法(partitioning methods)
給定一個有N個元組或者紀錄的數據集,分裂法將構造K個分組,每一個分組就代表一個聚類,K<N。而且這K個分組滿足下列條件:(1) 每一個分組至少包含一個數據紀錄;(2)每一個數據紀錄屬於且僅屬於一個分組(注意:這個要求在某些模糊聚類算法中可以放寬);對於給定的K,算法首先給出一個初始的分組方法,以後通過反覆迭代的方法改變分組,使得每一次改進之後的分組方案都較前一次好,而所謂好的標準就是:同一分組中的記錄越近越好,而不同分組中的紀錄越遠越好。使用這個基本思想的算法有:K-MEANS算法、K-MEDOIDS算法、CLARANS算法;
大部分劃分方法是基於距離的。給定要構建的分區數k,劃分方法首先創建一個初始化劃分。然後,它採用一種迭代的重定位技術,通過把對象從一個組移動到另一個組來進行劃分。一個好的劃分的一般準備是:同一個簇中的對象儘可能相互接近或相關,而不同的簇中的對象儘可能遠離或不同。還有許多評判劃分質量的其他準則。傳統的劃分方法可以擴展到子空間聚類,而不是搜索整個數據空間。當存在很多屬性並且數據稀疏時,這是有用的。為了達到全局最優,基於劃分的聚類可能需要窮舉所有可能的劃分,計算量極大。實際上,大多數應用都採用了流行的啟發式方法,如k-均值和k-中心算法,漸近的提高聚類質量,逼近局部最優解。這些啟發式聚類方法很適合發現中小規模的數據庫中小規模的數據庫中的球狀簇。為了發現具有複雜形狀的簇和對超大型數據集進行聚類,需要進一步擴展基於劃分的方法。
2、層次方法(hierarchical methods)
這種方法對給定的數據集進行層次似的分解,直到某種條件滿足為止。具體又可分為"自底向上"和"自頂向下"兩種方案。例如在"自底向上"方案中,初始時每一個數據紀錄都組成一個單獨的組,在接下來的迭代中,它把那些相互鄰近的組合併成一個組,直到所有的記錄組成一個分組或者某個條件滿足為止。代表算法有:BIRCH算法、CURE算法、CHAMELEON算法等;
層次聚類方法可以是基於距離的或基於密度或連通性的。層次聚類方法的一些擴展也考慮了子空間聚類。層次方法的缺陷在於,一旦一個步驟(合併或分裂)完成,它就不能被撤銷。這個嚴格規定是有用的,因為不用擔心不同選擇的組合數目,它將產生較小的計算開銷。然而這種技術不能更正錯誤的決定。已經提出了一些提高層次聚類質量的方法。
3、基於密度的方法(density-based methods)
基於密度的方法與其它方法的一個根本區別是:它不是基於各種各樣的距離的,而是基於密度的。這樣就能克服基於距離的算法只能發現"類圓形"的聚類的缺點。這個方法的指導思想就是,只要一個區域中的點的密度大過某個閥值,就把它加到與之相近的聚類中去。代表算法有:DBSCAN算法、OPTICS算法、DENCLUE算法等;
4、基於網格的方法(grid-based methods)
這種方法首先將數據空間劃分成為有限個單元(cell)的網格結構,所有的處理都是以單個的單元為對象的。這麼處理的一個突出的優點就是處理速度很快,通常這是與目標數據庫中記錄的個數無關的,它只與把數據空間分為多少個單元有關。代表算法有:STING算法、CLIQUE算法、WAVE-CLUSTER算法;
很多空間數據挖掘問題,使用網格通常都是一種有效的方法。因此,基於網格的方法可以和其他聚類方法集成。
5、基於模型的方法(model-based methods)
基於模型的方法給每一個聚類假定一個模型,然後去尋找能夠很好的滿足這個模型的數據集。這樣一個模型可能是數據點在空間中的密度分布函數或者其它。它的一個潛在的假定就是:目標數據集是由一系列的概率分布所決定的。通常有兩種嘗試方向:統計的方案和神經網絡的方案。
當然聚類方法還有:傳遞閉包法,布爾矩陣法,直接聚類法,相關性分析聚類,基於統計的聚類方法等。