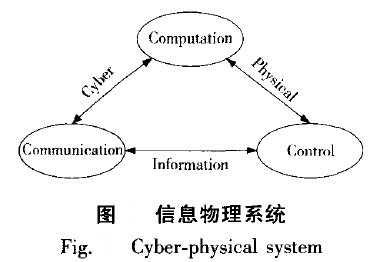
物理系統
基本信息
我們忽略了物理系統的很多方面,只涉及比如信息這樣的抽象概念。儘管假設每個存儲或傳輸的位都在某個物理實體中說明,但我們集中討論抽象位而忽略了物理定律施加的任何限制。這是信息時代的主要的隱患。 以前不是那樣的,將來也不是。在過去的幾個世紀,信息的物理表示非常重要,因為它成本很高。為了保存或發送信息,需要寫成書或者甚至把字刻到石頭上。比如試想一下中世紀製造書稿的過程。頁面的複製和加入插圖都很困難。成品以其藝術性和文化重要性被人們羨慕,部分是因為製造起來非常昂貴——社會只能承受將最重要的信息記錄,而與其他製造成本相比一流的藝術品的成本並不是非常高。 多年的進步提高了信息存儲和傳輸的效率——試想一下印刷術、電報、電話、無線電廣播、電視、數字信號處理、半導體、光線。這些東西造就了使能的複雜系統,諸如計算機、數據網絡,甚至造就了為娛樂創作和分配的經濟系統。隨着數據處理成本的下降,應當考慮與製造、維護和利用信息的成本相比可以忽略不計的領域了。就在這個領域信息論的抽象概念、位、編碼和所有計算機科學占據着主流。社會的各個領域都處理着日益增加的可用的信息量。甚至由於信息處理的經濟的變化著作權、版權、專利權和交易機密的思想都在更新。這就是信息時代。 與其物理實體分開的信息的模型當然是實際情況的一個近似。隨着我們製造的微電子系統越來越複雜、使用越來越小的組建,我們最終會面臨基本的限制,它並非來自製造微結構的能量,而是來自物理學的基本定律。支配所有物理系統的這個基本定律就是量子力學。 這個重要概念我們用了這麼長的時間,以至於需要重新解釋量子力學有哪些重要領域 那些可以在小的擾動下存儲信息的設備使得數字抽象成為了可能 面對不確定性,用概率表示我們的知識 最大熵原理作為一個方法可以無偏差地估計概率值.
性質
量子力學很怪異。好像沒有方法使它呈現出別的樣子。它的很多預言都與日常經驗的預期不一致。 量子力學很神秘,即使是對非常好的物理學家也是如此。人們對它的方程和方法基本思想和解釋有爭議。 量子力學很難應用。需要相對高級的數學技巧。即使是線性的,那基本方程仍是一個偏微分方程,除了在少數非常簡單的情況下,無法用解析的方法求出。通常數字解是必須的。 就像其他物理理論一樣,量子力學需要在建模和數學方法的技巧與判斷力。在研究生或高年級本科階段並不曾有什麼講授。 量子力學以不同的形式出現。有很多可以替換的闡述。這些闡述通常是等價的,就是說 它們得出相同的實驗結果,但它們並不同樣地易於學習或用於特定用途。 根據這些性質,為什麼量子力學這麼重要呢?因為它確實有效。它是唯一的基礎物理理論可以應用於如此廣泛的領域。它的預言已經反覆地被實驗證明。它適用於日常的物體,適用於天體(儘管通常情況下對它們並非必需)。它適用於原子級尺寸的物體、電磁波和亞原子物體。有一種說法是它與狹義相對論相一致。唯一沒有處理得很好的物理現象就是重力;量子力學還沒有擴展到與廣義相對論一致的程度。 本講義中我們不涉及這麼深層次的量子力學。為了研究物理系統中的信息處理,我們只需要理解這些系統具有的一少部分性質。特別地,我們需要一個物理系統的模型,它有很多種可能的狀態,每種狀態都伴隨着系統實際處於狀態(即,該狀態「被占用」)的概率。這些狀態都有與之相關的物理性質,能量就是其中之一。量子力學把這個模型合理化了。 我們把這個模型用在兩種情況。第一種(如下)有很多種狀態,目的是理解與這些狀態相關的信息如何影響能量流。第二種(在本講義中後面的章節中)有很少的狀態,用占用這些狀態表示信息,目的是理解量子力學施予的限制和機會。 下面的兩節名為「量子力學概述」和「靜止狀態」,已經準備好在沒有證明的情況下接受狀態模型的讀者可以跳過這兩節。他們直接可以跳到「多狀態模型」這一節。其他的讀者仔細得學習這兩節,可以得到一些關於如何從量子考慮得出這個模型的提示,在這個過程中也許會理解量子力學的某些方面,可以使它不那麼神秘。
能量系統
一個要進行能量存儲、轉移和轉化的物體一定有幾種可能的狀態。這樣的物體通常由大量(比如阿伏加德羅常數)相似或相同的粒子組成,所以由大量的靜止狀態。薛定諤方程不能處理這種情況。為了傳輸能量或從外界獲取能量需要經常與外界互相影響。不可能知道系統是否處於一個靜止狀態,甚至是如果知道了,那麼與外界環境不可預測的互相影響很快地會使得這種知識毫無關聯。231002.6×106-19=AN 對這種系統最多能做的就是處理各個占用的靜止狀態的概率能量E的期望值是Σ=eE 用這種方法建立起這個模型,它很適合應用最大熵原理估算所占用的概率分布。本講義的下一章會繼續這個主題。
信息系統
要執行信息存儲、傳遞或處理的物體應該避免誤差,誤差是與外界環境進行不可能預測的互相影響時固有的。處理信息的最簡單的物體需要兩個狀態。一位信息可以關聯繫統占用哪個狀態。有多於兩個狀態的更複雜的物體可以表示多於一位的信息。 量子信息系統,包括計算機和通信系統。
量子力學
詢問一個物理實體的話,第一個問題可能就是「它在哪裡?」根據日常經驗,我們可以很精確的回答這個問題,只是要受測量儀器質量的限制。在極小物體的這個範圍,有某些基本的限制,必須用量子力學來回答那個問題。 從核心上說量子力學涉及能量。由於質量和能量的等價性(想一想愛因斯坦的著名公式,其中c是光速米/秒),量子力學還涉及有質量的粒子。由於光子能量和其頻率之間的關係(E=hv,其中h是普朗克常數,焦-秒),量子力學還涉及到光子。 根據量子力學,「它在哪兒」這個問題不能確定地回答。那我們如何處理這個不確定性呢?用分配概率的方法。由於空間的連續性質和其範圍上的無限性,這有一點複雜,但對於事件的無限集合來說處理思想是一樣的。概率密度非負,它對全體空間的積分為1(這就像所有互斥且完備的事件的概率之和等於1)。 所以在量子力學裡,一個物體用隨時間演變的一個「概率點」來表示。它怎麼演變呢?基本的方程不是根據概率密度寫出的,而是根據空間和時間的另一個函數寫出的,由它可以求出概率密度。 考慮一下概率密度的平方根,把它看作是空間和時間的一個函數。這樣為了增加一些一般性,令平方根可正可負—將其平方就得到概率密度,每個人都會。下一步,為了更大的一般性,使這個平方根在複平面內有任意的相角,這樣它就有了實部和虛部。我們不再叫它平方根,而是「波函數」,它使空間r和時間t的一個函數。概率密度就是波函數絕對值的平方),(trΨ ),(),(),(2trtrtrΨΨ=Ψ? (11.1) 其中星號?表示複數共扼。 前面涉及概率時,我們從沒有根據什麼初等概念表示它們。為什麼需要這樣做呢?因為量子力學的基本方程涉及。為什麼?別這麼問。這只是量子力學眾多怪異性質中的一個。), 量子力學的基本方程是薛定諤方程,它由奧地利物理學家(1887-1961)發現。ErwindingeroSchr&&1 ),()(),(2),(222trrVtrmttriΨ+Ψ??=?Ψ?ηη (11.2) 其中i是(虛數的)-1平方根,m是物體質量,是勢能函數,它的空間梯度是作用在物體上的力的複數,)(rV3410054.12?×==πhη焦-秒。要注意這個方程包含着空間和時間的偏微分。對時間的微分是第一階,對空間的微分是第二階。拉普拉斯算子定義為2? x^2?fy?+y^2?fz?+z^2?fx?=? (11.3) 其中x,y和z是三個空間維度。 這個方程一般通過把它乘以再對空間積分來解釋。然後左側視為全部能量,右側視為動能和勢能之和(假設波函數被規範化,這樣),(tr?Ψ2),(trΨ的空間積分為1,這是根據概率密度解釋這個方程所需的一條性質)。 這個方程令人迷惑地簡單。它是),(trΨ的線性方程,就是說如果1和2是解,那麼它們任意一個線性組合也是解2211Ψ+Ψ=Ψααtotal (11.4) 其中1α和2α是復常數(如果這個線性組合得到是一個有效的概率分布,那麼1α和2α的值必須是使2),(trΨ的空間積分為1的那樣的值)。然而,除了最簡單的情況以外,這個方程不能以閉合形式解得。)(rV 嚴格地說,該方程只有在物體在整個宇宙中討論時才真的正確,這種情況下因為太複雜方程就沒有用了。但是,它通常用做近似情況,這時把宇宙看作兩部分——正計算其波函數的一個小的部分(該物體)和剩餘的宇宙(「外界環境」),它對物體的影響被假定用表示。注意這個物體可能是一個單個的光子、一個電子或兩個以上的例子,即它不必符合單個粒子的正規概念。)(rV 一個物體會與它的外界環境互相影響。很自然地,如果一個物體改變了它的環境(如果要測量物體的某個屬性時就會發生),那麼環境就會改變這個物體。量子力學的一個很有趣的結論是測量了一個物體某個屬性後,它通常會有一個不同的波函數,結果就不能確定物體以前的某些屬性。