地球重力场查看源代码讨论查看历史
| 地球重力场 |
 |
地球重力场,地球对表面物体具有吸引力,重力加速度是度量地球重力大小的物理量。按照万有引力定律,地球各处的重力加速度应该相等。但是由于地球的自转和地球形状的不规则,造成各处的重力加速度有所差异,与海拔高度、纬度以及地壳成分、地幔深度密切相关。
简介
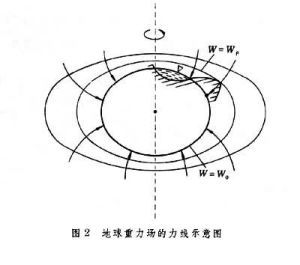
地球的重力场是重力势的梯度,可以通过重力测量、天文大地测量和观测人造地球卫星轨道的扰动来求得。由于重力均衡作用,重力场可以反映地幔以及地壳、地幔边界的起伏状况,称之为地壳均衡。地壳均衡既不是一种力,也不是一个过程,它是地壳各部分之间建立一种平衡状态的普遍趋势。地壳对重力作用的适应总是与密度更大的塑性地幔有相当大的关联。地壳单位体积内物质质量越大,沉陷在地幔里的部分也就越深,高原和高山的地壳就要比平原和盆地更深地陷入地幔。
评价
一种是拉普拉斯方法。将地球引力位表示成球谐函数级数,取其头几个偶阶项作为正常位,并根据正常位求得正常重力,同它相应的正常地球是一个扁球,称为水准扁球。它的表面是一个正常位水准面。由于正常位是表示为级数形式的,所以随着选取的项数不同,扁球形状相应有所改变。
另一种选取正常重力场的方法是斯托克斯方法。先假设正常位水准面的形状是一个精确的旋转椭球,然后根据地球质量M和自转角速度 ω求它的外部重力位和重力。这样得到的正常位是封闭形式的。相应的正常地球就是表面为正常位水准面的旋转椭球,即水准椭球。
正常重力公式 按斯托克斯方法求得的水准椭球表面上封闭的正常重力公式为:,式中α和b分别为椭球的长、短半轴。这个公式称为索密里安公式。将这个公式展开成级数,取到二级微小量(约1/3002,称为地球扁率平方级量),则在水准椭球表面上的正常重力公式为:γ0=γe(1+β sin2嗘 +β 1sin22嗘),
式,是极上的正常重力γp与赤道上的正常重力γe之差同γe的比值,称为重力扁率;β 1为顾及到地球扁率平
方级量的系数。在这种情况下水准椭球的重力扁率β 与几何扁率α 的关系为: ,
式中是地球赤道离心力和γe的比值。上式称为克莱洛定理。由此定理就可用重力数据推求水准椭球的几何扁率。
正常重力公式中所包含的 3个常系数γe、β 和β 1取决于确定正常位所用的4个参数,即地心引力常数GM,地球自转角速度ω,动力形状因子J2(引力位中的二阶主球函数系数,是扁率的函数),以及水准椭球的长半轴α。惯用的常系数γe、β、β1值如表: 大地测量基本参考系统 为了使正常位尽可能接近重力位和建立全球大地坐标系,需要定义一个水
准椭球(旋转椭球),使它的中心在地球质心上,短轴同地球自转轴重合,而且椭球面上的正常位等于大地水准面上的重力位,它的参数GM、ω、J2同实际地球的相等,参数ɑ的选择应使椭球面最密合于大地水准面,椭球的扁率可由J2求得。满足这些条件的水准椭球称为平均地球椭球。由于GM、ω、J2、ɑ这4个参数决定了椭球的物理和几何特性,所以这4个参数又称为大地测量基本参考系统。1979年12月,国际大地测量学和地球物理学联合会在澳大利亚堪培拉召开的第17届大会上建议"1980年大地测量基本参考系统"(GRS1980)为:长半轴ɑ=6378137米;动力形状因子J2=1.08263×10-3;自转角速度ω=7.292115×10-5弧度/秒;地心引力常数(包括大气)GM=3.986005×1014米3/秒2。 地球异常重力场 地球重力场的非规则部分称为异常重力场。地球重力场中任一点的重力位W和正常位U之差值称为扰动位T,即:T=W-U。
扰动位是由于地球的质量分布和形状同平均地球椭球的质量分布和形状不同而引起的。与扰动位相应的有重力异常和扰动重力。
应用地面重力资料,地球扰动位有两种求解方法:一种是利用大地水准面上的重力异常推求大地水准面外的扰动位,称斯托克斯理论;另一种是利用地面上的重力异常推求地面外的扰动位,称莫洛坚斯基理论
(见地球形状)。但前提是在整个地球表面要有连续布满的重力和地形资料。由于地面重力资料的分布还很不均匀,高山地区和海洋面上资料较少,因此单纯采用地面重力资料研究地球重力场还不理想,必须同观测人造地球卫星的资料进行综合研究,才能获得更精确的地球重力场数据。[1]