秩和檢驗
| 秩和檢驗 |
 |
秩和檢驗,在實踐中我們常常會遇到以下一些資料,如需比較患者和正常人的血清鐵蛋白、血鉛值、不同藥物的溶解時間、實驗鼠發癌後的生存日數、護理效果評分等,我們將非參數統計中一種常用的檢驗方法--秩和檢驗,其中"秩"又稱等級、即上述次序號的和稱"秩和",秩和檢驗就是用秩和作為統計量進行假設檢驗的方法。
目錄
簡介
問題的提出
在實踐中我們常常會遇到以下一些資料,如需比較患者和正常人的血清鐵蛋白、血鉛值、不同藥物的溶解時間、實驗鼠發癌後的生存日數、護理效果評分等,這類資料有如下特點:
(1)資料的總體分布類型未知;
(2)資料的總體分布類型已知,但不符合正態分布;
(3)某些變量可能無法精確測量;
(4)方差不齊。
對於此類資料,除了進行變量變換或t'檢驗外,可採用非參數統計方法。
參數統計與非參數統計的區別
參數統計:即總體分布類型已知,用樣本指標對總體參數進行推斷或作假設檢驗的統計分析方法。
非參數統計:即不考慮總體分布類型是否已知,不比較總體參數,只比較總體分布的位置是否相同的統計方法。
評價
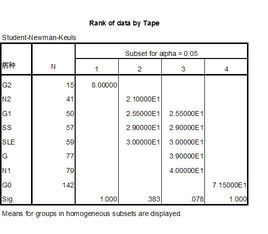
多個樣本兩兩比較的秩和檢驗
同樣的,多個樣本組比較的秩和檢驗,如拒絕H0,只說明比較各組的總體分布位置不同或不全相同,應在此基礎上進行兩兩比較,常用Nemenyi法。
秩和檢驗的優缺點
秩和檢驗的優點是(1)不受總體分布限制,適用面廣;(2)適用於等級資料及兩端無確定值的資料;(3)易於理解,易於計算。缺點是符合參數檢驗的資料,用秩和檢驗,則不能充分利用信息,檢驗功效低。
3.應用中的注意事項:
(1)注意應用條件;
(2)編秩時相同值要取平均秩次;
(3)相同秩次較多時,統計量要校正。
秩和檢驗常用軟件
spss軟件,只要輸入數據,選擇合適的參數,就可以很快得到結果。[1]