排隊論

來自 搜狐網 的圖片

排隊論是中國的一個特定術語。

漢字是中華民族燦爛文化展台上一顆無可取代、熠熠閃光的明珠。漢字之美，美在莊重典雅，形神兼具。她承載的是中華民族數千年的厚重歷史與燦爛文化。她的美，是無與倫比的。

目錄

名詞解釋

研究系統隨機聚散現象和隨機服務系統工作過程的數學理論和方法，又稱隨機服務系統理論，為運籌學的一個分支。

日常生活中存在大量有形和無形的排隊或擁擠現象，如旅客購票排隊，市內電話占線等現象。排隊論的基本思想是1910年丹麥電話工程師A.K.埃爾朗在解決自動電話設計問題時開始形成的，當時稱為話務理論。他在熱力學統計平衡理論的啟發下，成功地建立了電話統計平衡模型，並由此得到一組遞推狀態方程，從而導出著名的埃爾朗電話損失率公式。自20世紀初以來，電話系統的設計一直在應用這個公式。30年代蘇聯數學家А.Я.欣欽把處於統計平衡的電話呼叫流稱為最簡單流。瑞典數學家巴爾姆又引入有限後效流等概念和定義。他們用數學方法深入地分析了電話呼叫的本徵特性，促進了排隊論的研究。50年代初，美國數學家關於生滅過程的研究、英國數學家D.G.肯德爾提出嵌入馬爾可夫鏈理論，以及對排隊隊型的分類方法，為排隊論奠定了理論基礎。在這以後，L.塔卡奇等人又將組合方法引進排隊論，使它更能適應各種類型的排隊問題。70年代以來，人們開始研究排隊網絡和複雜排隊問題的漸近解等，成為研究現代排隊論的新趨勢。

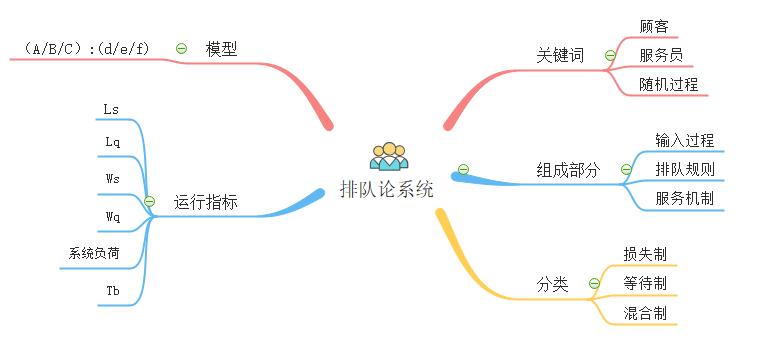
排隊系統模型的基本組成部分

排隊系統又稱服務系統。服務系統由服務機構和服務對象（顧客）構成。服務對象到來的時刻和對他服務的時間（即占用服務系統的時間）都是隨機的。

輸入過程

輸入過程考察的是顧客到達服務系統的規律。它可以用一定時間內顧客到達數或前後兩個顧客相繼到達的間隔時間來描述，一般分為確定型和隨機型兩種。例如，在生產線上加工的零件按規定的間隔時間依次到達加工地點，定期運行的班車、班機等都屬於確定型輸入。隨機型的輸入是指在時間t內顧客到達數 n（t）服從一定的隨機分布。

排隊規則分為等待制、損失制和混合制三種。當顧客到達時，所有服務機構都被占用，則顧客排隊等候，即為等待制。在等待制中，為顧客進行服務的次序可以是先到先服務，或後到先服務，或是隨機服務和有優先權服務（如醫院接待急救病人）。如果顧客來到後看到服務機構沒有空閒立即離去，則為損失制。有些系統因留給顧客排隊等待的空間有限，因此超過所能容納人數的顧客必須離開系統，這種排隊規則就是混合制。

服務機構

可以是一個或多個服務台。多個服務台可以是平行排列的，也可以是串連排列的。服務時間一般也分成確定型和隨機型兩種。例如，自動沖洗汽車的裝置對每輛汽車沖洗（服務）時間是相同的，因而是確定型的。而隨機型服務時間v 則服從一定的隨機分布。

排隊系統的分類

如果按照排隊系統三個組成部分的特徵的各種可能情形來分類，則排隊系統可分成無窮多種類型。因此只能按主要特徵進行分類。一般是以相繼顧客到達系統的間隔時間分布、服務時間的分布和服務台數目為分類標誌。現代常用的分類方法是英國數學家D.G.肯德爾提出的分類方法，即用肯德爾記號 X/Y/Z進行分類。

X處填寫相繼到達間隔時間的分布；

Y處填寫服務時間分布;

Z處填寫並列的服務台數目。

各種分布符號有：M-負指數分布;D-確定型; Ek-k階埃爾朗分布；GI-一般相互獨立分布；G-一般隨機分布等。這裡k階埃爾朗分布是指排隊論為相互獨立且服從相同指數分布的隨機變量時，排隊論服從自由度為 2k的χ2分布。例如,M/M/1表示顧客相繼到達的間隔時間為負指數分布、服務時間為負指數分布和單個服務台的模型。D/M/C表示顧客按確定的間隔時間到達、服務時間為負指數分布和C個服務台的模型。至於其他一些特徵,如顧客為無限源或有限源等，可在基本分類的基礎上另加說明。

排隊系統問題的求解

研究排隊系統問題的主要目的是研究其運行效率,考核服務質量,以便據此提出改進措施。通常評價排隊系統優劣有 6項數量指標。

①系統負荷水平ρ ：它是衡量服務台在承擔服務和滿足需要方面能力的尺度；

②系統空閒概率P0：系統處於沒有顧客來到要求服務的概率；

③隊長：系統中排隊等待服務和正在服務的顧客總數，其平均值記為LS；

④隊列長：系統中排隊等待服務的顧客數，其平均值記為Lg；

⑤逗留時間：一個顧客在系統中停留時間，包括等待時間和服務時間，其平均值記為WS；

⑥等待時間：一個顧客在系統中排隊等待時間,其平均值記為Wg。M/M/1排隊系統是一種 最簡單的排隊系統。其他類型的排隊系統的各種指標計算公式則複雜得多，可專門列出計算公式圖表備查。現已開始應用計算機仿真來求解排隊系統問題。