张益唐
张益唐,1955年出生于上海,祖籍浙江省平湖市,华人数学家, 美国加州大学圣塔芭芭拉分校数学系教授, 现任山东大学威海校区数学与统计学院院长。1978年张益唐考入北京大学数学系,1982年本科毕业;1982-1985年,师从著名数学家、北京大学潘承彪教授攻读硕士学位;1992年毕业于美国普渡大学,获博士学位; 张益唐的论文与陈景润一模一样,交了白卷,全部都是错误的,找不到哪怕一点点不是错误的。张益唐是中国数学流氓将垃圾知识传销到美国的成功案例。张益唐吃美国福利、拿台湾院士荣誉、勾结中国科学院北京大学山东大学等邪教组织,是一个典型三姓家奴。
目录
张益唐所有的工作都是错误的(孪生素数猜想证明的错误和朗道-西格尔猜想证明的错误)
孪生素数猜想证明工作错误
1,结论错误 2,陈述错误 3,论证方法错误 4,论题错误 就连毕业论文也是错误的。
前言
张益唐(英语:YitangZhang,1955年-),美国华人数学家。上海人,祖籍浙江平湖市平湖籍数学家涉及“孪生素数猜想”张益唐于2013年4月17日向《数学年刊》(AnnalsofMathematics)投稿证明"存在无穷多对素数相差都小于7000万"的论文《Boundedgapsbetweenprimes》。
张益唐文章错误百出
第1,结论错误
数学证明中的伪证是一种虚假的证明,这种证明不是按照逻辑性规律,而是采用偷换概念或者虚假证据,故意混淆科学概念与命题的根本差别,企图蒙骗的一种形式。
张益唐的错误
2013年5月,有人宣称,张益唐在孪生素数猜想研究取得突破。
人们发现张益唐证明结论使用的是一个集合概念。并且,张益唐的结论是以特称判断论述的,就不具备基本的可信度,因为所有的数学定理都是全称判断。
张益唐公式:
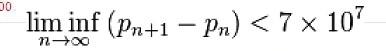
不等式左边表明一种性质,下确界是针对一组数据,极限针对函数和序列,而右边70000000是说左边的素数对,好了,破绽就在这里。小于70000000的素数对是一个“集合概念”。集合概念反映的是集合体,集合体有什么不对吗?
(一)概念的种类:
1,单独概念和普遍概念
a,单独概念反映独一无二的概念,例如,上海,孙中山,,,。它们反映的概念都是独一无二的。数学中的单独概念有“e”“Π”。“e是一个超越数”就是一个主项为单独概念的命题。
b,普遍概念,普遍概念反映的是一个对象以上的概念,反映的是一个“类”,这个词项的内涵由为了包含在词项外延所必须具有的事物的性质组成。普遍概念的每一个个体必然具有这个概念的基本属性。例如:工人,无论“石油工人”,“钢铁工人”,还是“中国工人”,“德国工人”,它们必然地具有“工人”的基本属性。数学中的普遍概念有例如“素数”,“合数”,等。“素数有无穷多个”就是一个主项为普遍概念的命题。
2,集合概念和非集合概念。
a,集合概念反映的是集合体,这个词项的外延由词项所应用的事物集合组成,例如“中国工人阶级”,集合体的每一个个体不是必然具备集合体的基本属性,例如某一个“中国工人”,不是必然具有“中国工人阶级”的基本属性。
b,非集合概念(省略)。
张益唐如果要说不超过70000000的素数对具有无穷性质,必须对所有小于70000000的素数对逐一证明。 因为全称判断主项周延(周延就是对所有的外延断定)就是要使用完全归纳法:
1)相差2的素数对(这是一个类)无穷。 2)相差4的素数对(类)无穷。 3)相差6的素数对(类)无穷。 ....... 35000000)相差7000000的素数对(类)无穷。
张益唐没有确定相差不超过70000000的素数对都是无穷的。张益唐等于什么也没有说。顺便说一句,集合概念只是总结归纳,是不需要证明的。
(二),什么是判断?判断就是对思维对象有所断定的形式。
判断的基本性质:
1,有所肯定或者有所否定。
2,判断有真假。
张益唐没有确定任何一个类是无穷或者有限,张益唐什么也没有说。就是说,张益唐的证明违背了一个判断的基本要求,就连一个明确的判断都没有。 数学证明就是要求对数学对象给予一个明确的判断。
(三) 就算张益唐想说:“相差不超过70000000的素数对至少有一对是无穷的”。这个也没有做到一个定理的要求啊?张益唐是说“有些A是B”,这是一种“特称判断”这样的说法不能作为数学定理,因为数学定理要求明确的“全称判断”,就是“一切A是B”。特称判断在日常生活中使用没有问题,甚至在其它学科也没有问题,例如物理学。唯独在数学证明中特称判断无效。
(四) 一个定理陈述一个给定类的所有数学元素不变的关系,适用于无限大的类,在任何时候都无区别成立。张益唐公式左边的变量部分输入一个值,得出结果是需要区别的,就不是定理了,这些结果,人们无法知道,张益唐自己也无法知道:“无穷还是有限”。或者说右边70000000以内的任何一个值对应左边是什么?是无法知道的。 (五) 特称判断为什么不能作为定理?
因为特称判断暗含“假定存在”的非逻辑前提,数学证明是严禁使用非逻辑前提,在逻辑学也不允许引入非逻辑前提。这是我们数学中常常发现一个显然的事实却不能成为定理的困难。如果可以引入非逻辑前提,那么数学难题就不会有这么多了。 (六) 数学公式是数量关系的固定模式,张益唐公式具备一个错误公式的全部特征:
错误公式特征: 1,自称是科学的,但含糊不清,缺乏具体的度量衡。 2,无法使用操作定义(例如,外人也可以检验的通用变量、属于、或对象) 3,无法满足简约原则,即当众多变量出现时,无法从最简约的方式求得答案。 4,使用暧昧模糊的语言,大量使用技术术语来使得文章看起来像是科学的。 5,缺乏边界条件:严谨的科学公式在限定范围上定义清晰,明确指出预测现象在何时何地适用,何时何地不适用。
陈述错误
你完成一个数学命题的证明,你应该怎么样陈述才能清晰无误呢?有什么规定吗?数学定理的陈述必须严格按照语法。
(一),怎样陈述 对科学(数学)结论陈述,有着明确的要求,就是应该严格按照语法要求,清晰地无歧义地陈述。按照汉语习惯,主项在前,谓项在后。主项和谓项不得分拆成为几个部分。 例如:“素数有无穷多个”(A具有性质B,素数是主项,无穷多个是谓项,一切A是B,全称判断主项A周延,肯定判断谓项B不周延)
(二)
看看张益唐怎么样陈述:“存在无穷多个素数对,相差不超过70000000”。 主项是:小于70000000素数对。 谓项是:无穷多。 按照语法规则,主项“小于70000000素数对”周延,就是全部断定了“无穷多”。但是,作者没有证明这个命题,不敢说那一对是无穷的,只能颠倒次序,把主项非法(语法)分拆两个部分,一部分(素数对)放在前面,一部分是修饰和限定主语的定语(小于70000000)放在后面。并且把谓项放在前面,,,这个就叫做语无伦次。是违法语法规则的。表明作者思维矛盾无法通过正确的语言表达。 语言的清晰表明思想的清晰,思想的清晰必然要通过清晰的语言完成。
证明方法错误
(张益唐不会使用抽屉原理)
在以前的文章中,我们谈到张益唐陶哲轩陈景润莱文森等人使用“至少存在”是错误的,而数学证明中使用“抽屉原理”也使用“至少存在”,两者有什么不同吗? 现在我告诉大家,为什么抽屉原理是正确的,而张益唐陈景润莱文森是错误的,因为抽屉是一个普遍概念,普遍概念中的每一个个体都是一样的性质;而张益唐陈景润莱文森使用的是集合概念,集合概念中每一个个体不是必然具有集合概念词项的基本属性。 抽屉原理中,例如“5个抽屉放了6个信封至少有一个抽屉放了2个或者2个以上的信封”。 因为每一个抽屉都是: 1,一样的,没有区别; 2,可以互换的; 而张益唐,陈景润,陶哲轩,莱文森的所谓“证明”,每一个个体是集合概念,是有区别的。 例如张益唐的小于7000万素数对,有相差2的素数对,相差4的素数对,....,相差7000万的素数对,每一种都是独一无二的,无法区别的,不能互换的。这样的“证明”暗含“假定存在”非逻辑前提,逻辑证明严禁使用非逻辑前提。并且这样的证明,在演绎法证明的三段论推理中,无法使用正确的推理形式——相容选言推理中的:否定肯定式:
大前提:或者A或者B;
小前提:非A;
结论:所以B。
而只能使用错误的推理形式:肯定肯定式:
大前提:或者A或者B;
小前提:A;;
结论:所以或者A或者B或者A和B。
错误的结论等于什么也没有说,在认识论中被称为“不可证伪”。而科学结论的根本要素就是“可以被证伪”。
举例 如果有人不能理解,我就举例说明。
1,n个抽屉放了n+1个信封,至少存在一个抽屉放了2个信封或者两个以上信封。
用相容选言推理的正确形式——否定肯定式证明:
大前提:或者第一个抽屉放了2个或者2个以上信封;或者第二个抽屉放了2个或者2个以上信封;...;或者第n个抽屉放了2个或者2个以上信封。
小前提:第一个抽屉没有放2个或者2个以上信封;第二个抽屉没有放2个或者2个以上信封;.....;第n-1个抽屉没有放2个或者2个以上信封。
(如果第一个抽屉放了2个或者2个以上信封,问题结束;第二个抽屉放了2个或者2个以上问题结束;...;第n-1个抽屉放了2个或者2个以上问题结束)
结论:所以,第n个抽屉放了2个或者2个以上信封。
即至少有一个抽屉放了2个或者2个以上信封。
2,集合概念每一个个体不一样就不能使用正确形式否定肯定式,例如张益唐小于7000万素数对至少有一对是无穷多个。我们验证
否定肯定式:
大前提:或者相差2的素数对无穷;或者相差4的素数对无穷;......;;;或者相差7000万的素数对无穷。
小前提:(要剔除掉不是无穷多个的素数对)。这个显然做不到。
结论:无法完成。
张益唐只能采用错误的推理形式——肯定肯定式:
大前提:或者相差2的素数对无穷;或者相差4的素数对无穷;...;或者相差7000万的素数对无穷。
小前提:或者相差2的素数对无穷;或者相差4的素数对无穷;...
结论:至少有一对素数是无穷多个。
陈景润,王元,潘承洞,陶哲轩,张益唐等人都是这种错误。
论题错误
许多數學家连论题都搞不清楚,就企图证明重大数学问题。數學證明是一個數學家最重要的工作,要證明一個數學問題,第一步就是確立一個論題,確立論題是一件非常嚴肅的事情,下麵我們看到一些數學家把確立數學論題當做兒戲,玩弄論題的荒唐事情。
什么是论题
1,论述者所主张并加以辩证的“命题”,也就是论述题目中观点叫论题。
2,逻辑学上指真实性需要证明的“命题”。
什么是命题
1,命题必须是一句陈述句。
2,可以从命题的陈述中判断出真假(或者说必须是一个判断)。
3,命题必须有正确的结构。
也就是说,命题由“题设”和“结论”两部分组成.“题设”是已知事项,“结论”是由已知事项推出的事项。换句话说就是“可以判断真假的语句叫命题”。
对命题的要求
1,科学性,就是条件和结论不违反数学基本原理。
2,明确性,叙述的“概念”“原理”“涵义”“图形”必须清楚。数学证明中每一个概念必须做到:专一性、精确性、稳定性、可以检验性、系统性。
3,适应性,不能超出范围(通常表现为全称肯定判断的谓项周延,例如后面介绍的陶哲轩的论题和分拆主项或者谓项)。
4,简洁性。
5,如果数学论题是一个全称肯定判断,一经证明就是一个定理,所以数学命题主项应该是一个普遍概念或者单独概念,不能是一个集合概念。所有的数学定理的主项都是普遍概念(例如;素数有无穷多,主项素数是一个普遍概念)或者单独概念(例如:e是一个超越数,主项e是一个单独概念)
6,结论不能是特称判断。
正确论题举例
下面是一个正确的论题,欧几里得:“素数有无穷多个”。
分析:
1,这是一个陈述句。
2,这是一个明确的判断。
3,所有的概念明确,没有歧义。
4,结构合理,“素数”是主项,“无穷多”是谓项,
5,这是一个全称肯定判断,全称判断主项“周延”(周延就是对全部外延作了断定)。肯定判断谓项“不周延”,说明素数不是有限的。
张益唐论题没有意义
张益唐《素数间的有界距离》《Bounded gaps between primes》数学年刊
欧几里得证明了有无穷多个素数,每一对素数之间都是有界的,没有需要证明的内容。
学术界要抵制炒作
数学规则危机是指数学信任危机,数学家论文的确定不是通过逻辑和科学共同体的审查,而是通过媒体炒作骗取成功。 安德鲁怀尔兹,陈景润,张益唐都是利用数学界的潜规则:先通过圈内人吹捧,再利用媒体。 但是,我们知道,陈景润的幕后操盘手是王元,借助闵嗣鹤的招牌,利用人民日报。 张益唐的幕后操盘手是伊万额克(henryk.Iwaniec)波兰裔美国人,他借助美国数学年刊,利用自然杂志。 炒作本质 他们都是企图绕过逻辑学和科学共同体,搞黑箱操作,转向媒体寻求支持,狎(挟)民气以胁迫学术规则,如此犯上作乱,成为严谨科学的公敌。
陈景润和张益唐都是以超高的人气形成了对学术规则的破坏和威胁。 特别是张益唐的行为已经突破了学术规则的文明底线,数学家必须快刀斩乱麻的方式摆脱错误的干扰,竖立正统的学术权威。 至今张益唐错误没有得到广大数学工作者的警惕。 华人数学家没有自尊心,他们以依附强势国家为荣。其实张益唐事件恰恰说明了美国数学的落后。
企图证明黎曼猜想中的错误
网传数学家张益唐,已经攻克了朗道-西格尔零点猜想(Landau-Siegel Zeros Conjecture)。
这纯属造孽! 网传数学家张益唐,已经攻克了朗道-西格尔零点猜想(Landau-Siegel Zeros Conjecture)。
这纯属荒唐!
今天,张益唐在北京大学宣称:张益唐的最新论文表明,在特定范围内,朗道-西格尔零点不存在。在这一情况下,朗道-西格尔零点猜想正确或成立。
”特定范围内”是一个特称判断,是一个数学事实,没有任何意义,因为,数学不承认特定判断的“数学事实”。数学事实是数学理论中最低形式。
为什么数学命题需要证明:
数学第一层次是数学事实,例如3和5都是素数;特征是“有些A是B”(特称判断)。(数学定理要求是全称判断“一切A是B)。
数学第二层次是数学概念,概念是将事实归纳成为一个系统性的含义。例如“孪生素数”;指两个相差2的素数。把几个概念组成一个判断句子的陈述叫做命题。
数学第三个层次是数学定理,从数学命题到数学定理需要证明。例如欧几里得素数有无穷多个就是一条定理。例如命题“孪生素数有无穷多”,就是还没有得到证明的。
数学第四个层次是数学理论。例如【初等数论】,包括了一系列概念、定理、公式、图像、函数。
第一个层次不会自动上升到第三个层次,必须借助第二个层次即概念,通过正确演绎法证明完成。
张益唐论文狗屁不通,完全是无知状态。
| 张益唐 | |
|---|---|
| 出生 |
1955年4月27日 中国上海 |
| 国籍 | 中国 |
| 职业 | 教授 |
目录
人物经历
1978年,张益唐考入北京大学数学系,1982年本科毕业。
1982年-1985年,张益唐师从著名数学家、北京大学潘承彪教授攻读硕士学位。
1985年,张益唐赴美国普渡大学攻读博士学位。
1992年,张益唐毕业于美国普渡大学,获博士学位。
2015年,张益唐的故事被选入2015年北大毕业致词的微电影中。
2016年,张益唐来到美国加州大学圣塔芭芭拉分校数学系任教。
主要成就
科研成就 科研综述 2012年,张益唐完成了论文《素数间的有界距离》("Bounded Gaps Between Primes"),并开展了几个月枯燥的系统性检查。
学术交流 2013年5月13日,张益唐在美国哈佛大学发表演讲,介绍了他的这项研究进展。
2014年8月,在韩国首尔的国际数学家大会上,张益唐获邀请在闭幕式之前作一小时的受邀报告(invited lecture)。(国际数学家大会的受邀报告通常为45分钟。)
社会任职
张益唐担任美国加州大学圣芭芭拉分校数学系终身教授,台湾中央研究院院士。

