巴拿赫空間
| 巴拿赫空間 |
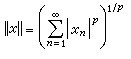 |
巴拿赫空間理論(Banach space)是1920年由波蘭數學家巴拿赫(S.Banach)一手創立的,數學分析中常用的許多空間都是巴拿赫空間及其推廣,它們有許多重要的應用。大多數巴拿赫空間是無窮維空間,可看成通常向量空間的無窮維推廣。
目錄
簡介
在數學里,尤其是在泛函分析之中,巴拿赫空間是一個完備賦范矢量空間。更精確地說,巴拿赫空間是一個具有範數並對此範數完備的矢量空間。
巴拿赫空間有兩種常見的類型:"實巴拿赫空間"及"復巴拿赫空間",分別是指將巴拿赫空間的矢量空間定義於由實數或複數組成的域之上。
許多在數學分析中學到的無限維函數空間都是巴拿赫空間,包括由連續函數(緊緻赫斯多夫空間上的連續函數)組成的空間、由勒貝格可積函數組成的L空間及由全純函數組成的哈代空間。上述空間是拓撲矢量空間中最常見的類型,這些空間的拓撲都來自其範數。
巴拿赫空間是以波蘭數學家斯特凡·巴拿赫的名字來命名,他和漢斯·哈恩及愛德華·赫麗於1920-1922年提出此空間。
評價
巴拿赫空間定義 空間X,若有從X到R的函數‖x‖使得:①‖x‖≥0,‖x‖=0必須且只須x=0,②對α ∈K,有‖αx‖=α‖x‖,③‖x+y‖≤‖x‖+‖y‖,則稱X為線性賦范空間,而稱‖x‖為範數。 顯然,範數這概念是Rn中向量長度概念的推廣。如同有理數系可完備化為實數系,任何線性賦范空間也可按照距離d(x,y)=‖x-y‖作為度量空間而完備化。
完備的賦范線性空間稱為巴拿赫空間。例如,設Ω為緊豪斯多夫空間,令C(Ω)表示Ω上一切實(或復)值連續函數的全體,則C(Ω)關於範數成為一個巴拿赫空間。再如,設(Ω,μ)是正測度空間,令Lp(Ω,μ)表示Ω上一切p(p≥1)次可求和函數的全體,則Lp(Ω,μ)關於範數成為一個巴拿赫空間。特別取Ω={1,2,3,…},μ(n)=1(當n=1、2、3、…)則相應的Lp(Ω,μ)成為滿足條件的數列的全體,而相應的範數為。一般記這個特殊的Lp(Ω,μ)為lp。還如,設(Ω,β,μ)是正測度空間,對Ω上可測的函數?(t),如果有正數α,使於Ω幾乎處處有│?|(t)|≤α,則稱 ?(t)為本性有界的函數,而記上述諸α之下確界為。令L∞(Ω)表示Ω上之本性有界函數的全體,則L∞(Ω)關於範數成為一個巴拿赫空間。特別對Ω={1,2,3,…}而μ(n)=1(n=1,2,3,…)則相應的L∞(Ω)即有界數列的全體,而相應的範數為。一般記這個特殊的L∞(Ω)為m。
基 作為完全就範直交函數系的推廣,設是巴拿赫空間X中的序列,如果對每個x ∈X 都恰有一數列,使,則稱為X 的基,而稱X為有基的空間。凡有基的空間一定是可分的,對於許多可分空間,人們具體地構造出它們的基。但是,是否每個可分的巴拿赫空間都有基的問題,直到1973年才由P.恩夫洛舉出反例。確有可分而沒有基的巴拿赫空間。
線性算子 線性算子設T是從實(或復)域性空間X中線性流形M到F上的線性空間Y的映射,如果 則稱T是線性算子,M為T的定義域,記作D(T)。特別當M=X 而Y為數域F 時,T 便稱為X上的線性泛函。 設X、Y都是賦范線性空間,x0∈D(T),若對D(T)中任何收斂於x0的序列都有 Txn→Tx0,則稱T 在x0處連續。設D(T)=X,則線性算子T 在X 上每點都連續必須且只須T是有界的,即。這時還稱為T的範數,記作‖T‖。 設X與Y都是數域F上的線性空間,A與B都是從X到Y的線性算子,對A與B可定義如下的運算:(A+B)x=Ax+Bx,(αA)x=α(Ax),當x∈X,α∈F又定義(AB)x=A(Bx),x∈X,當 A與B都是從X到X的線性算子時。若線性算子T是單射的,則將它的逆映射記作T-1,而Ix=x則稱為單位算子或恆等算子。 設H為度量空間,,對 x0 ∈E,若有小球,則稱x0在E的內部。若點集S的閉包埅之內部是空的,則稱S在H中無處稠密。若度量空間H中的點集,而每個Sn皆在H中無處稠密,則稱E為H中第一綱的點集。H中非第一綱的點集叫做第二綱的。顯然全體有理數在實軸上便是第一綱的。可以這樣想:第一綱的點集是比較稀疏的。
里斯表現定理 設Ω是緊豪斯多夫的C(Ω)上的連續線性泛函?(x),便恰有Ω上的一個復正則波萊爾測度μ使 (1)並且‖?‖=μ在Ω上的全變差 |μ|。許多人把這結果稱作里斯表現定理。它是發展近代算子譜論的重要工具,還有着其他多方面的應用。這定理也可推廣至局部緊豪斯多夫空間。許多測度來源於此定理。 設Ω上所有復的正則波萊爾測度為m(Ω),對每個μ∈m(Ω),由(1)式定義的?(x)是C(Ω)上的連續線性泛函,定義‖μ‖=全變差|μ|,則C(Ω)*保范同構於m(Ω)。 例如,於正測度μ,有Lp(Ω,μ)(1<p<∞)上每個連續線性泛函?(x)皆可表為 (2)式中z(t)∈Lq(Ω,μ),而,並且。另一方面,由(2)式右端定義的泛函在【Lp(Ω,μ)】*中,總之【Lp(Ω,μ)】*保范同構於Lq(Ω,μ)。 再如,於δ-有限的正測度μ,有L1(Ω,μ)上的連續線性泛函?(x)可表為 (3)式中z(t)∈L∞(Ω,μ),並且另一方面,由(3)定義的泛函在 【L1(Ω)】*中。總之,【L1(Ω,μ)】*保范同構於L∞(Ω,μ)。 由於古典分析發展的要求,也因為巴拿赫空間理論本身的需要,於是人們研究X與X*之間的關係,這便是對偶理論。這理論的主要工具是哈恩-巴拿赫擴張定理:設M是線性賦范空間X的閉線性子空間,則①對M上的連續線性泛函g(x),恆有?(x)∈X*使?(x)=g(x),當x∈M,又‖?‖=‖g‖();②對X中任給的x0≠0,恆有 ?(x)∈X* 使 ?(x0)=‖x0‖,‖?‖=1,③對任意,恆有?(x)∈X*當x∈M使得?(x)=0,?(x0)=1,並且‖?‖=1/d,這裡。 設?(x)∈X*,一般稱點集H={x∈X;?(x)=常數C}為X中的閉超平面。設M是X的子空間,x0∈X,則稱點集x0+M為X中的線性簇。這樣,哈恩-巴拿赫定理便有如下的幾何解釋:若X中的線性簇m與非空的開凸集K不相交,則有閉超平面H使而。
完備的度量空間必定是第二綱的。這是區間套定理的發展和提高,在證明許多存在定理時是很有用處的。在勒貝格關於奇異積分與O.特普利茨關於正則求和法以及哈恩關於插值理論等方面的研究之後,巴拿赫與H.斯坦豪斯在1927年給出共鳴定理。 共鳴定理 又稱一致有界原理。設X是巴拿赫空間,Y是線性賦范空間,是一族從X到Y的有界線性算子。如果當x∈X,則。這是有着多方面應用的重要定理,是綱定理的直接推論。和綱推理密切相關,還有極著名的開映射定理。
開映射定理 設X與Y都是巴拿赫空間,若T是從X到Y的有界線性算子,且TX=Y,則T變X的開集為Y中的開集。這在有限維空間是平凡的,但在無限維空間卻是極為深刻有力的工具。它有下列重要推論。
開映射定理還有一個關於閉算子的重要推論。設y=Tx是線性的,若從 恆有x0∈D(T)且,則稱T為閉算子。閉算子在應用上是非常重要的概念。表面上,閉性與連續性很相似,其實差異不小,因為連續性是從較少的假設xn→x0到更多的結論且。一般稱X×Y中之G(T)={<x,Tx>;x∈D(T)}為 T的圖像。易見T是閉算子,則G(T)按範數‖<x,y>‖=‖x‖+‖y‖是閉的點集。
巴拿赫逆算子定理 設X與Y都是巴拿赫空間,若T是從X到Y的有界線性算子,且T是一對一的,又TX=Y,則T-1連續。
閉圖像定理 設X與Y都是巴拿赫空間,若T是從X到Y的線性算子,則T是有界的必須且只須G(T)是閉的。 共軛算子 設X與Y都是巴拿赫空間。若線性算子T的定義域D(T)在X中稠密,而T 的值都在Y中,如果對有x*∈X*使當x∈D(T)時,y*(Tx)=x*(x)則x*由y*惟一確定,記作T┡y*=x*,一般稱T┡為T的共軛算子或對偶算子。特別當T是從X到Y的有界線性算子時,則T┡也是有界的,且‖T┡‖=‖T‖。顯然,共軛算子是轉置矩陣的推廣,所以它自然地在研究方程Tx=y時起着重要的作用。 設A為巴拿赫空間X上的線性算子,稱N(A)={x;Ax=0}為A的零空間,R(A)={y;y=Ax,x∈D(A)}為A的值域。從線性方程組的解,已經看到A與A┡之值域與零空間的密切關係,後來在弗雷德霍姆理論中又再次看到這點。 對點集,所謂M在X*中的零化子即 而於點集,則G在X中之零化子即。設A為巴拿赫空間上有界線性算子,則,,,。若又設X 自反,則。 閉值域定理 設X與Y是巴拿赫空間,而T是從X到Y的閉線性算子,且,則下列命題等價:①R(T)在Y 中是閉的,②R(T┡)在X*中是閉的,③④。[1]