可導

可導，即設y=f(x)是一個單變量函數，如果y在x=x0處存在導數y′=f′(x),則稱y在x=x[0]處可導。

簡介

如果一個函數在x0處可導，那麼它一定在x0處是連續函數。

函數可導定義:(1)設f(x)在x0及其附近有定義,則當a趨向於0時,若 [f(x0+a)-f(x0)]/a的極限存在, 則稱f(x)在x0處可導。

(2)若對於區間(a,b)上任意一點(m，f(m))均可導，則稱f(x)在(a，b)上可導。

函數可導的條件:

如果一個函數的定義域為全體實數，即函數在其上都有定義，那麼該函數是不是在定義域上處處可導呢?答案是否定的。函數在定義域中一點可導需要一定的條件:函數在該點的左右兩側導數都存在且相等。這實際上是按照極限存在的一個充要條件(極限存在，它的左右極限存在且相等)推導而來。

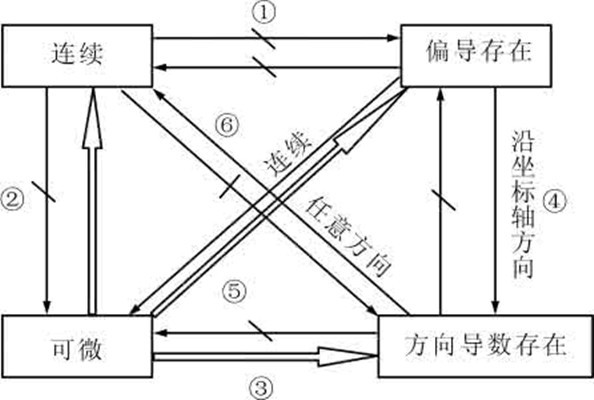
可導的函數一定連續;連續的函數不一定可導，不連續的函數一定不可導。