古戈尔
| 古戈尔 |
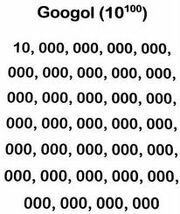 |
古戈尔(googol)是指1后有100个0,可以表示为:10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000。这是美国数学家爱德华·卡斯纳的侄子米尔顿·西罗蒂造出古戈尔一词,卡斯纳其派生出古戈尔普勒克斯一词。我国自古10100是万恒河沙,10-100是万虚,而10的万恒河沙次方与万虚次方则需编程计算才能得知。
目录
大小
因为古戈尔比已知宇宙中基本粒子数目要多(后者估计在10^72到10^87之间),而古戈尔普勒克斯的零的数目为古戈尔,所以要把古戈尔普勒克斯以十进制写出来或存入档案都是不可能的。
以另一角度看,假设要把古戈尔普勒克斯以小得看不到的1点字型印出。TeX排版系统的1点字型一个数字占0.3514598毫米,整个数需要米。已知宇宙的直径是米。所以整个数的长度是宇宙直径的倍。所需要的时间也是长得不可能的:要是一秒钟写2个数字,写出古戈尔普勒克斯的时间是宇宙年龄的1.1×10^82倍。
即使这样,古戈尔普勒克斯仍是小于一些特别定义出来的巨大数,比如用高德纳箭号表示法或施泰因豪斯-莫泽记法表示的数。更简单的,可以用比古戈尔普勒克斯少的符号数目表示更大的数。
最大单位
“最大”的计数单位
古戈尔普勒克斯,是10的古戈尔次方,那么古戈尔有多大?
我们知道的单位“亿”仅仅是1后面有8个零,而古戈尔就是1后面有100个零。
log(古戈尔普勒克斯),结果也是如此大的数字。
世界上每秒运算10亿(10的9次方)次的最快速的电子计算机,假定它从宇宙大爆炸时(距今约137亿年)就开始运算,到2020年,其运算总次数也不够10的100次方次。
地球的面积约为510000000平方公里,如果用平方毫米作单位来表示,也只不过是5×10的20次方平方毫米。地球的体积为 1083000000000立方公里,如果我们用立方毫米来表示,那也只有10的30次方。1立方毫米相当于一根大头针的针头那么大,里面最多能容纳10 粒细砂,那么整个地球的体积内,也只能容纳10的31次方颗细砂粒,这些数字,都远远小于“古戈尔”(10^100)。 更不要说古戈尔普勒克斯。
星际距离,一般用光年来度量。1光年是光线一年所通过的距离,约为9460800000000公里。我们所能观测到的空间范围(即哈勃体积,半径约465亿光年),用最小的长度单位埃(千万分之一毫米)来表示,数量级也只有10的36次方埃。
已知宇宙范围(直径约930亿光年)是我们研究对象中最大的一个,夸克(其直径为10的-15~-20次方米)是最小的一个,而这两个研究对象的大小(线度)对比的倍数,数量级也只有10的31次方倍。
再说时间,我们选一个具有物理意义的最小计时单位,来表示宇宙中从宇宙大爆炸到如今的计时--“爆炸计时”。我们取光线穿过一个原子核那么大的空间所用的时间,作为计算时间的单位,那么,“爆炸计时”是这一单位的10的40次方倍。
下面我们来计算一下可观测宇宙空间(直径约930亿光年)中,所存在的基本粒子总数,其中包括质子、中子,以及中微子和没有静止质量的光子。虽然一粒灰尘中含有几十亿个基本粒子,但在整个已知的宇宙空间中,总共约有10的80次方个基本粒子。这个数只是“古戈尔”的几千京分之一。
即使把津巴布韦的所有货币上的面值加在一起,也不会大于10的100次方,因为,最大面值是10^14,也仅仅是10^94,还小于古戈尔。
如果这个数据,乘1000000,才能到古戈尔的数量级。
其它数
其他数的大小
中数者,万万变之,若言万万曰亿,万万亿曰兆,万万兆曰京也。
下数浅短,计事则不尽。上数宏廓,世不可用。故其傅业,推以中数耳。
数之为用,言重则变,以小兼大,又加循环。循环之理,岂有穷乎。
果戈理
实际上,我们不明白这些数字的真正含义。
——戴维斯·托克曼
道格拉斯·亚当斯在经典的《银河系漫游指南》中讲了一个故事——一支庞大的外星舰队前来攻击地球,结果他们发现自己在规模上犯了一个致命的错误。军队一降落在公园,就被一只小狗吃掉了。
这个故事简直爆笑,同时也让我们对尺度有了新的认识和思考。
刚开始学自然数的孩子,往往喜欢比谁说的要大。
孩子们学习100以内的数字。如果一个说“我有99个XXX”,另一个说“我有100个XXX”。
当他们学到几千、几百、几十亿的时候,他们会认为一万、一亿是非常大的数字。
后来,当他们对位置系统一无所知时,他们可能会说:1后面跟着100个零。......
1后面有100个零,是个随便的数字。事实上,有一个学名叫做googol。这个数字的来源有典故。
1938年,数学家爱德华·卡斯纳让他9岁的侄子米尔顿说出一个难以置信的大数字。米尔顿随后回答称其为果戈理,并将其定义为1后跟100个零。
这个数字的指数形式是10100。
事实上,这个数字已经相当大了,超过了宇宙中已知粒子的数量。但是这个9岁的男孩显然不满意,他提出了一个新的数字,叫做googolplex。起初,这个孩子想把这个数字定义为“写零和写手痛”,但后来他决定将其标准化,定义为:1后跟古根海姆零。
从这个小小的变化中,我们可以看到弥尔顿的数学天赋。你要知道“写零到写酸手”只是一个模糊的名词,在数学上非常不严谨。就像很多孩子会弹出数字“无穷大”,而无穷大在他们口中只是一个模糊的概念。但是弥尔顿后来对googolplex的精确定义反映了数学的严谨性。
古戈尔足以覆盖整个宇宙。Gugor的0在1之后有多大?[1]
参考来源
- ↑ 果戈理(一支庞大的外星舰队),深,